发布日期:2018-10-09 17:23 来源:活性炭网 作者:活性炭网 浏览数:
该研究包括开发一种内部扩散模型,在多孔粒子中吸附,以估计其有效扩散系数。 为此目的,将颗粒悬浮在处于过渡状态的等温完全搅拌反应器中(封闭系统)。 所采用的模型基于内
该研究包括开发一种内部扩散模型,在多孔粒子中吸附,以估计其有效扩散系数。为此目的,将颗粒悬浮在处于过渡状态的等温完全搅拌反应器中(封闭系统)。所采用的模型基于内部多孔表面上的吸附平衡,并假设外部浓度在外部转移电阻不存在时随时间变化。使用有限差分技术数值求解所提出的模型方程。对商业活性炭上的染料吸附的实验浓度曲线进行平滑以适合所提出的模型。获得了实验理论概况之间的良好一致性。
| 关键词 | |
| 动力学吸附; 媒体多孔; 数值解; 扩散系数 | |
| 符号 | |
| c:孔隙溶液浓度,mg / l | |
| C:流体相溶质浓度,mg / l | |
| C 0:初始浓度,mg / l | |
| K L:Langmuir吸附参数,l / mg | |
| D e:扩散系数,cm 2 / s | |
| K L:传质系数,cm / s | |
| q m:每单位吸附剂体积的吸附容量,mg / cm 3 | |
| r:粒子的径向坐标,cm | |
| R p:粒子半径,cm | |
| T:时间,嗯 | |
| V:溶液体积,cm 3 | |
| V p:颗粒体积,cm 3 | |
| m:固体质量,mg | |
| γ:与吸附等温线相切的截距 | |
| ε p:颗粒孔隙率 | |
| ρ:表观密度颗粒,g / cm 3 | |
| 介绍 | |
| 文献中多孔中间的动力学吸附在研究中占据了一席之地。这种现象可以在溶液中引起含有活性炭(多孔中间)。化学工程中的许多重要过程包括在颗粒或流体球体内扩散的模型。因此,对这些扩散方程的精确但仍然计算简单的解决方案非常重要。自Glueckauf的经典近似解决方案以来,吸附过程中的扩散已经进行了许多研究[ 1]。在该解决方案中,球形颗粒内的质量传递通过假设质量传递速率线性地取决于球体内的平均浓度与表面浓度之间的差异以及恒定的假设(时间独立的)来描述。 masstransfer系数。从那时起,该假设已被广泛用于吸附器建模。此外,已经表明线性驱动力假设(LDF)等于假设颗粒内的浓度分布。这两种方法被用于缓解时间相关的材料余额在吸收剂[复杂溶液2 - 6 ]。在本文中,我们用数值方法和分析方法研究扩散方程的解。 | |
| 扩散模型 | |
| 球形颗粒内扩散的建模通常是与化学工程(例如吸附)相关的许多过程的建模的重要部分。描述扩散的微分方程的精确解是一个非常复杂的任务,涉及无限级数的计算。鉴于吸附剂研究的高度多孔结构和对不同着色剂的相对低的吸附容量,使用孔扩散模型来拟合数据。我们假定粒子是球形且半径为R的p,它们具有内孔隙ε p,以及局部平衡在所述孔的液体和吸附剂表面之间的小珠内的每个点的存在。外部传质阻力被忽略了。 | |
| 通过这些假设,模型由以下守恒方程和边界条件表示。对于粒子 | |
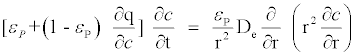 (1) (1) |
|
| 在该等式中,D e和q分别表示有效孔扩散率和吸附相中的浓度。 | |
| 有了边界条件 | |
 (1a)的 (1a)的 |
|
| r = R p,c = C(1b) | |
| t = 0,c = 0(1c) | |
| 'c'表示孔隙流体中的浓度。 | |
| 我们第一次认为平衡是瞬时的,并且孔隙流体c中的浓度等于初始浓度C 0。 | |
| 我们发现着色的吸附很好地表现为Freundlich等温线。因此,方程左侧的括号内的术语。(1)可以近似为 | |
 (2) (2) |
|
| 当K F代表Freundlich常数时。 | |
| Crank-Nicolson的隐式方法用于数值模拟不同D e值的模型方程,我们使用Matlab logitiel。如果我们用时间表示浓度的关系,我们发现随后出现各种扩散常数(图1-4)。 | |
| 当平衡不是瞬间发生并且外部流体C变量中的浓度随时间变化时,模型由守恒方程(1)和边界条件(1a),(1b),(1c)表示,并由容器中液体的方程式 | |
 (3) (3) |
|
| t = 0,C = C 0 (3a) | |
| 在这些等式中,p = 3V p / VR p是每单位体积液体的颗粒的表面积,C是外部流体中的浓度。在均衡c = C时,因此,在等式左边的括号中的项。(1)可以从吸附等温线获得。当吸附等温线为线性时,(1)和(3)可以通过分析求解。吸附等温线是通过[ε表示p C +(1-ε p)Q] = MC +γ,其中m和γ是常数,我们得到 | |
 (4) (4) |
|
| 哪里 | |
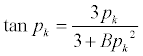 (4a)的 (4a)的 |
|
| 在这些等式中,q∞ = B(mC 0 +γ)/(1 + B)并且B = V / mV p。 | |
| 然而,在等温线是非线性并且应用有限浓度步骤的情况下,通常需要数值解。在这一部分中,我们发现着色的吸附很好地表现为langmuir等温线。因此,方程左侧的括号内的术语。(1)可以近似为 | |
 (5) (5) |
|
| 其中K L代表Langmuir吸附参数。 | |
| q m表示每单位吸附剂体积的吸附容量。 | |
| 验证模型 | |
| 一些工作对通过多孔固体吸附溶液中有机分子或矿物离子的动力学研究感兴趣。作为Grzegorczyk等人的示例工作。[ 7 ],关于用多孔固体吸附氨基酸,使用表1规定的操作条件给出了非常重要的结果。我们建议使用这些结果来测试和验证我们工作中开发的模型。Grzegorczyk等。[ 7 ],还使用正交配置的方法,基于有限元的使用,数值求解扩散方程D e的各种值的扩散方程模型。 | |
| 在第一次模拟中,Grzegorczyk等人发表的实验结果。[ 7 ],我们的模型对各种有效扩散系数值进行了平滑处理。值得注意的是,该模型与Grzegorczyk等人的实验非常吻合。[ 7 ]。 | |
| 图5-7表示通过我们的Grzegorczyk三种活性炭实验的动力学模型进行平滑。 | |
| 因此我们的模型和Grzegorczyk等人的模型估计了有效扩散系数的值。[ 7 ],对于三种类型的活性炭,如表2所示。 | |
| 对于三种类型的活性炭,通过Grzegorczyk等人的模型估计的有效扩散系数的值。与我们的模型估计的数量级具有相同的数量级,这进一步证明了我们的模型与Grzegorczyk等人的模型之间的一致性。[ 7 ]。 | |
| 诺芮特型活性炭对苯酚的吸附 | |
| 为了通过在水性介质中吸附苯酚来消除,在该部分中使用诺芮特型平均直径的活性炭等于940μm,所使用的酚水溶液的体积为800ml,其中一种添加质量W = 1600Mg。将活性炭加热至固定的温度θ= 40℃。用同样的方法,使用曲柄尼科尔森的隐式方法进行数值求解模型方程d的不同值ê,我们使用Matlab的logitiel,R的值p,ε p,Q 米,K 大号,ρ,V和给出关于Najjar的实验结果的V p [8],诺芮特活性炭。一个代表诺芮特可吸附苯酚溶液的相对分数随各种浓度初始C 0的时间变化,得到图8-10。 | |
| 值得注意的是,我们的模型与实验点一致。人们注意到我们的模型估计表3中各种初始浓度C 0的有效扩散系数值。 | |
| 对于Norit型活性炭上苯酚的吸附,当初始浓度C 0增加时,有效扩散系数De的值减小,则可以推断出有效扩散系数取决于初始浓度。图11表示根据log C 0的( - log D e)的演变。 | |
| 为了在生成的诺芮特型活性炭上吸附苯酚,有效扩散率De在与初始浓度C 0相反的方向上变化。可以推断,有效扩散系数取决于初始浓度。因此,现在用诺芮特表示溶液中苯酚C 0的初始浓度大的时间,诺芮特吸附的苯酚水溶液的相对分数,然后得到图12和13.注意,对于溶液C 0中的高初始苯酚浓度= 200 mg / l和C 0 = 300 mg / l,该模型没有完全遵循实验点。 | |
| 结论 | |
| 这项工作代表了粒子多孔固体动力学吸附的数值研究,当吸附等温线为线性时,扩散方程可以通过分析求解,但当等温线是非线性时,一般需要数值解。使用几种方法来获得解决方案,例如Crank-Nicolson隐含的方法。然后将计算出的扩散模型的数值结果与平滑实验曲线的实验和扩散系数D e进行比较。 | |